The density of Bernoulli Convolutions in 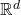\mathbb{R}^d

The video animates the density of the Bernoulli convolution \sum_{j=0}^\infty \xi_j \lambda^j for \xi_j \sim \mathrm{Unif}(\{0,1\}) and \lambda a Garsia number of degree three. The density is displayed in \mathbb{R}^3 under the embedding S: \mathbb{Q}(\lambda) \to \mathbb{R}^3, S(x)=(x, \mathrm{Re}(\tau(x)), \mathrm{Im}(\tau(x))) for \tau the complex conjugate. The density in \mathbb{R}^3 is natural to look at because different points in the sum are part of a lattice and separated (of order c^{-j}). So, the underlying structure of the density is easier to see in \mathbb{R}^3 than when only considering points in \mathbb{R}.
In the animation, the Garsia number \lambda is the one corresponding to a root of x^3+x^2-x-2. The sum is cut after j=28 and all 2^{28} points are plotted in \mathbb{R}^3. The axis corresponding to the real root is the time direction. More animations are available (just send me a mail if you’re interested). For other Garsia numbers, the convergence is much slower, so the animations look less refined, though.